Продолжение...

Формирование модели технологического процесса.

Методика выполнения работы.

Для решения поставленной задачи с целью анализа условий эрозии твёрдой корки формирующегося слитка производилось сопряжённое моделирование и решение ряда задач.

Гидравлическое моделирование опорожнения стопорного ковша и заполнения изложницы производили с использованием системы уравнений [1]:

где h_к - высота металла в ковше, h_ф- высота металла в изложнице, f_к - сечение стопорного стакана, F_к - сечение сталеразливочного ковша, F_ф - сечение изложницы, - коэффициент расхода из ковша, - время.

В случае прямой заливки металла из ковша в изложницу скорость струи на уровне зеркала металла определяется уравнением:

где h_c - высота падения струи, вытекающей из ковша.

При использовании промежуточной воронки скорость вытекания металла из неё составляет

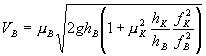где h_В - высота металла в воронке, - коэффициент расхода в воронке, f_В_–входноесечение зеркала в воронке. Скорость струи на уровне зеркала металла в этом случае будет

В силу того, что <1 и <1, применение промежуточной воронки существенно снижает скорость струи, если соотношение сечений достаточно мало (<3), однако, основным фактором является высота падения струи. По этой причине в процессе заливки скорость струи весьма существенно снижается по мере заполнения изложницы.

Гидродинамическое моделирование заполнения изложницы проводили на основе решения уравнений Навье-Стокса с учётом изменения входной скорости V_c струи заливаемого металла [2]:

дополняемых уравлением неразрывности .

В качестве граничных условий задавали:

на твёрдых поверхностях и плоскостях - условия непротекания и свободного скольжения;

во входящем или выходящем потоках жидкости - условие свободного протекания 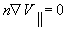, а также , если скорость потока задана, и в противном случае, где n - нормаль к граничной поверхности;

в зоне затвердевания сплава (t_c<t<t_л) принимали, что скорость течения V обращается в ноль при достижении температурной границы t₀ образования непрерывной твёрдой фазы.

Моделирование теплообмена в системе расплав - поддон - водоохлаждаемая изложница производили на основе решения уравнения теплопроводности Фурье с конвективным слагаемым, учитывающим перенос тепла при перемещении расплава со скоростью V, определяемой гидродинамическими условиями [3]:

где a – температуропроводность металла, в которой объёмная теплоёмкость С учитывает выделение тепла в интервале кристаллизации сплава:

где С_ж, С_т - объёмная теплоёмкость жидкой и твёрдой фаз, m - доля твёрдой фазы, L - объёмная скрытая теплота кристаллизации, t_л , t_с - температуры ликвидуса и солидуса сплава.

Начальные условия задавали по температуре заливки стали t_зал, а также температуре изложницы и поддона t_н_.

Условия теплоотдачи на границе с внешней средой Т_с задавали выражением, основанным на уравнении Ньютона и описывающим теплообмен на поверхности при известном после расчёта коэффициенте полной теплоотдачи :

где Т - температура в граничной точке формы, t - время, a=l /C - коэффициент температуропроводности, l - коэффициент теплопроводности.

Наряду с вынужденной конвекцией расплава возникновение температурных перепадов по сечению залитой части изложницы приводит к появлению сил естественной конвекции вследствие изменения плотности расплава при понижении температуры, характеризуемого коэффициентом объёмной усадки

В результате нагрева стенки водоохлаждаемой изложницы до температуры, превышающей температуру кипения t_к охлаждающей воды, возникает пристеночное кипение, проходящее стадии пузырькового и пленочного кипения с переменным коэффициентом теплоотдачи, величина которого зависит от свойств жидкости и режима кипения. Для пузырькового режима кипения задавали [4]:

где - плотности пара и жидкости; - теплопроводность, вязкость и поверхностное натяжение жидкости, t_к- температура кипения, t_с - температура стенки изложницы.

При пленочном кипении на вертикальной поверхности коэффициент теплоотдачи определяется соотношением [4]:

В условиях пристеночного кипения жидкости граничное условие задавали соотношением:

где - теплопроводность изложницы, grad t - градиент температуры на наружной поверхности изложницы.

На границах раздела металл - изложница и изложница - поддон образуется зазор, толщина d которого зависит от условий усадки наружной корки или задаётся конструктивными соображениями (шероховатость поверхности, косое прилегание поддона и т.д.). Теплообмен в зазоре определяется условиями контакта между соприкасающимися поверхностями, которые характеризовали коэффициентом h , обозначающим долю поверхности с идеальным контактом. Общая формула, описывающая термическое сопротивление R_T в зазоре, определяет соотношение между лучистым теплообменом и теплопроводностью в газовом зазоре и по плоскости плотного контакта поверхностей [5]:

где: , ,

l _М, l _В - теплопроводность металла и вещества газового зазора, Т_П- температура поверхности тела, Т_С - температура окружающей среды, С - приведённый коэффициент лучеиспускания системы тел, С₁ - коэффициент лучеиспускания первого тела, С₂ - коэффициент лучеиспускания второго тела, С₀- коэффициент лучеиспускания абсолютно чёрного тела, F₁ и F₂ - площади поверхностей охватываемого и охватывающего тел, - коэффициент черноты.

Влияние конвекции на величину коэффициента теплопроводности расплава учитывали введением коэффициента конвекции К_t [6]:

l = l ₀(1 + K_{t * D}T),

где l ₀ - теплопроводность покоящегося расплава, D Т - локальное значение перегрева металла над ликвидусом. Эрозионное воздействие потока на образующуюся твёрдую корку учитывали введением коэффициента размыва К_V [7] по формуле Cp=C₀( 1 + K_{V *}V ),

где С₀ - объёмная теплоёмкость покоящегося расплава, Сp - эффективная теплоёмкость в области размыва, V - скорость потока расплава, ориентированного по касательной к твёрдой корке.

Для описания процесса фазового превращения в стали при затвердевании использован аппарат термодинамического моделирования сплавов [8], обеспечивающий возможность вычислить для многокомпонентных сплавов значения критических температур, энтальпии, теплоты кристаллизации и теплоемкости в зависимости от температуры и состава сплавов. В таблице приведены расчетные значения ряда теплофизических характеристик (температуры ликвидуса T_Л и солидуса T_С, объемная теплота кристаллизации Q, объёмная теплоёмкость в жидком C_Ж и твёрдом C_Тсостоянии) для исследованных марок сталей.

Таблица

Теплофизические характеристики сталей

Марка стали	T_Л, ^оC	Tс, ^оC	Q, МДж/м³	Cж, МДж/м³К	Cт, МДж/м³К
08ГДНФЛ	1516	1488	1945	5.74	4.84
40Х	1494	1435	2045	5.77	4.83
40ХН	1492	1432	2050	5.76	4.82
40ХН2МА	1490	1428	2045	5.75	4.81
38ХН3МФА	1487	1426	2015	5.73	4.80
20Н3ДМА	1497	1456	1970	5.72	4.81
9ХС	1513	1460	1930	5.78	5.10

Решение представленной системы уравнений осуществляли численным методом, используя основные модули программного комплекса “POLYCAST” [9], подвергшиеся значительной модернизации применительно к особенностям поставленной задачи. В результате решения получены численные значения распределения температур и скорости циркуляции расплава в различные моменты времени по сечению заливаемой изложницы, а также по толщине стенки изложницы и поддона (рис.2 ¸ 27), позволяющие количественно анализировать условия образования и эрозии твердой корки металла на стенках изложницы.